
Олимпиада «Сириус» ответы, вопросы по Математике 9 класс, школьный этапа Всероссийской олимпиады 2 группа от 14 октября 2025 года. Официальный вариант с вопросами по химическим элементам, простым и сложным веществам.
Школьный этап Сириус по Математике для 2-ой группы 14 октября 2025 г.
Вопросы и ответы 9 класс
Задание 1. Есть 90 литров смеси, в которой доли красной, зелёной и синей красок равняются 35%, 25% и 40% соответственно. Сколько литров красной и зелёной краски нужно добавить, чтобы получилась смесь с 40% красной, 30% зелёной и 30% синей красок? Синюю краску добавлять нельзя.
Красной: л
Зелёной: л
→ Раскрыть ответ
Задание 1. Есть 70 литров смеси, в которой доли красной, зелёной и синей красок равняются 20%, 35% и 45 % соответственно. Сколько литров красной и зелёной краски нужно добавить, чтобы получилась смесь с 25% красной, 40% зелёной и 35% синей красок? Синюю краску добавлять нельзя.
→ Раскрыть ответ
Задание 1. Есть 90 литров смеси, в которой доли красной, зелёной и синей красок равняются 25%, 20% и 55 % соответственно. Сколько литров красной и зелёной краски нужно добавить, чтобы получилась смесь с 30% красной, 25% зелёной и 45% синей красок? Синюю краску добавлять нельзя.
→ Раскрыть ответ
Задание 1. Есть 30 литров смеси, в которой доли красной, зелёной и синей красок равняются 35%, 40% и 25% соответственно. Сколько литров красной и зелёной краски нужно добавить, чтобы получилась смесь с 40% красной, 45% зелёной и 15% синей красок? Синюю краску добавлять нельзя.
→ Раскрыть ответ
Задание 2. В таблице 6×6 отметили несколько клеток. После этого слева от каждой строки написали, сколько клеток от левой границы до первой отмеченной клетки в этой строке свободны. Аналогичные числа записали сверху, справа и снизу. После этого числа сверху, а также отметки в клетках стёрли.
Найдите количество отмеченных клеток. Восстановите числа, которые были записаны сверху.
→ Раскрыть ответ
Задание 3. Два равносторонних треугольника с параллельными сторонами расположены так, как показано на рисунке. Оказалось, что расстояния между параллельными сторонами треугольников равны 3√3. Найдите разность периметров этих треугольников.
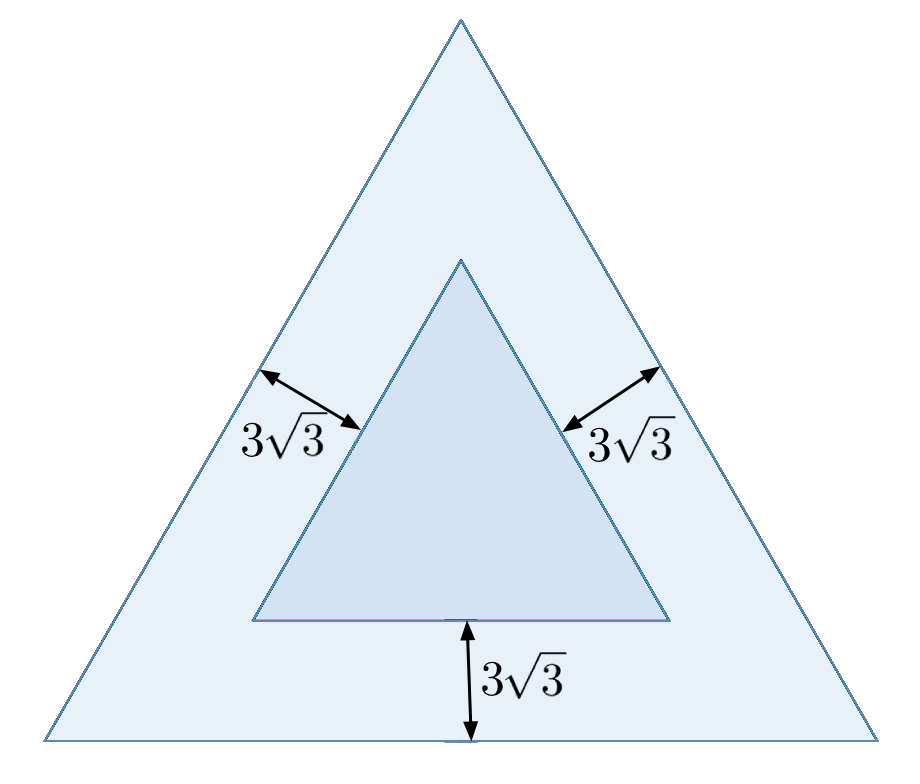
Задание 4. Числа 3, 6, 11, 16, 23 и 31 разбили на три группы по два числа так, что выполняются следующие условия:в первой группе оказались только простые числа,во второй группе сумма чисел делится на 3,сумма чисел в третьей группе больше половины от общей суммы.
Какие числа в какой группе?
3
6
11
16
23
31
Первая группа
Вторая группа
Третья группа
→ Раскрыть ответ
Задание 4. Числа 2, 6, 11, 15, 23 и 31 разбили на три группы по два числа так, что выполняются следующие условия: в первой группе оказались только простые числа, во второй группе сумма чисел делится на 3, сумма чисел в третьей группе больше половины от общей суммы. Какие числа в какой группе?
→ Раскрыть ответ
Задание 4. Числа 3, 8, 11, 17, 22 и 31 разбили на три группы по два числа так, что выполняются следующие условия: в первой группе оказались только простые числа, во второй группе сумма чисел делится на 3, сумма чисел в третьей группе больше половины от общей суммы. Какие числа в какой группе?
→ Раскрыть ответ
Задание 4. Числа 2, 6, 11, 15, 23 и 31 разбили на три группы по два числа так, что выполняются следующие условия: в первой группе оказались только простые числа, во второй группе сумма чисел делится на 3, сумма чисел в третьей группе больше половины от общей суммы. Какие числа в какой группе?
→ Раскрыть ответ
Задание 5. Дан треугольник АВС с прямым углом С. Окружность с центром в А, проходящая через С, пересекает гипотенузу в точке Е, а окружность с центром в В, проходящая через С, пересекает гипотенузу в точке Д. Найдите ED, если AD = 15, BE = 30.
→ Раскрыть ответ
Задание 5. Дан треугольник АВС с прямым углом С. Окружность с центром в А, проходящая через С, пересекает гипотенузу в точке Е, а окружность с центром в В, проходящая через С, пересекает гипотенузу в точке Д. Найдите ED, если AD = 12, BE = 54.
→ Раскрыть ответ
Задание 5. Дан треугольник АВС с прямым углом С. Окружность с центром в А, проходящая через С, пересекает гипотенузу в точке Е, а окружность с центром в В, проходящая через С, пересекает гипотенузу в точке Д. Найдите ED, если AD = 16, BE = 50.
→ Раскрыть ответ
Задание 5. ан треугольник АВС с прямым углом С. Окружность с центром в А, проходящая через С, пересекает гипотенузу в точке Е, а окружность с центром в В, проходящая через С, пересекает гипотенузу в точке Д. Найдите ED, если AD = 14, BE = 112.
→ Раскрыть ответ
Задание 6. В квадрате 5×5 расставили натуральные числа от 1 до 25, каждое по одному разу, так, что суммы чисел в каждой строке, каждом столбце и каждой из двух диагоналей совпали. Оказалось, что в центре стоит число 18. Чему может быть равна сумма чисел в отмеченных клетках?

Задание 6. В квадрате 5×5 расставили натуральные числа от 1 до 25, каждое по одному разу, так, что суммы чисел в каждой строке, каждом столбце и каждой из двух диагоналей совпали. Оказалось, что в центре стоит число 17. Чему может быть равна сумма чисел в отмеченных клетках?
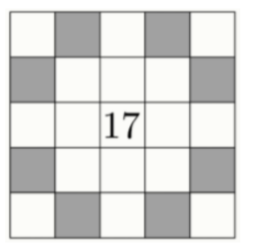
Задание 6. В квадрате 5×5 расставили натуральные числа от 1 до 25, каждое по одному разу, так, что суммы чисел в каждой строке, каждом столбце и каждой из двух диагоналей совпали. Оказалось, что в центре стоит число 17. Чему может быть равна сумма чисел в отмеченных клетках?
→ Раскрыть ответ
Задание 6. В квадрате 5×5 расставили натуральные числа от 1 до 25, каждое по одному разу, так, что суммы чисел в каждой строке, каждом столбце и каждой из двух диагоналей совпали. Оказалось, что в центре стоит число 9. Чему может быть равна сумма чисел в отмеченных клетках?
→ Раскрыть ответ
Задание 6. В квадрате 5×5 расставили натуральные числа от 1 до 25, каждое по одному разу, так, что суммы чисел в каждой строке, каждом столбце и каждой из двух диагоналей совпали. Оказалось, что в центре стоит число 9. Чему может быть равна сумма чисел в отмеченных клетках?
→ Раскрыть ответ
Задание 7. Натуральные числа а, в таковы, что число 9a+10b/a+2b тоже натуральное. Чему может быть a+2b a равно отношение a\b? Укажите все подходящие варианты. Каждый ответ записывайте b в отдельное поле, добавляя их при необходимости.
→ Раскрыть ответ
Задание 8. На квалификационное соревнование, по результатам которого отбираются участники на областной чемпионат, подали заявки 80 команд. Отбор происходит по следующей схеме. У каждой команды есть некоторый счёт побед и поражений (изначально 0-0). В каждом матче принимают участие две команды с одинаковым текущим счётом, и одна из них побеждает, а другая проигрывает (ничьих не бывает). Если команда набирает 3 поражения, она выбывает из отбора. Если команда набирает 3 победы, она выходит в основную часть тоже прекращает участие в квалификационном соревновании. Турнир оканчивается, И когда судьба каждой команды будет определена. Сколько команд попадёт на областной чемпионат? Сколько будет сыграно матчей?
→ Раскрыть ответ
Задание 8. На квалификационное соревнование, по результатам которого отбираются участники на областной чемпионат, подали заявки 112 команд. Отбор происходит по следующей схеме. У каждой команды есть некоторый счёт побед и поражений (изначально 0-0). В каждом матче принимают участие две команды с одинаковым текущим счётом, и одна из них побеждает, а другая проигрывает (ничьих не бывает). Если команда набирает 3 поражения, она выбывает из отбора. Если команда набирает 3 победы, она выходит в основную часть И тоже прекращает участие в квалификационном соревновании. Турнир оканчивается, когда судьба каждой команды будет определена. Сколько команд попадёт на областной чемпионат? Сколько будет сыграно матчей?
→ Раскрыть ответ
Задание 8. На квалификационное соревнование, по результатам которого отбираются участники областной чемпионат, подали заявки 96 команд. Отбор происходит по следующей схеме. У каждой команды есть некоторый счёт побед и поражений (изначально 0-0). В каждом матче принимают участие две команды с одинаковым текущим счётом, и одна из них побеждает, а другая проигрывает (ничьих не бывает). Если команда набирает 3 поражения, она выбывает из отбора. Если команда набирает 3 победы, она выходит в основную часть тоже прекращает участие в квалификационном соревновании. Турнир оканчивается, когда судьба каждой команды будет определена. И Сколько команд попадёт на областной чемпионат? Сколько будет сыграно матчей?
→ Раскрыть ответ
Задание 8. На квалификационное соревнование, по результатам которого отбираются участники на областной чемпионат, подали заявки 128 команд. Отбор происходит по следующей схеме. У каждой команды есть некоторый счёт побед и поражений (изначально 0-0). В каждом матче принимают участие две команды с одинаковым текущим счётом, и одна из них побеждает, а другая проигрывает (ничьих не бывает). Если команда набирает 3 поражения, она выбывает из отбора. Если команда набирает 3 победы, она выходит в основную часть и тоже прекращает участие в квалификационном соревновании. Турнир оканчивается, когда судьба каждой команды будет определена. Сколько команд попадёт на областной чемпионат?
→ Раскрыть ответ