
Тренировочная работа СтатГрад №4 по Информатике для 11 класса, вариант № ИН2410402 задания, ответы — это уникальный материал для подготовки к ЕГЭ, разработанный в соответствии с требованиями ФИПИ и форматом реального экзамена.
Тренировочная работа СтатГрад №4 по Информатике для 11 класса
→ Скачать все варианты, решения
Вариант ИН2410402 задания и ответы для подготовки к ЕГЭ по Информатике
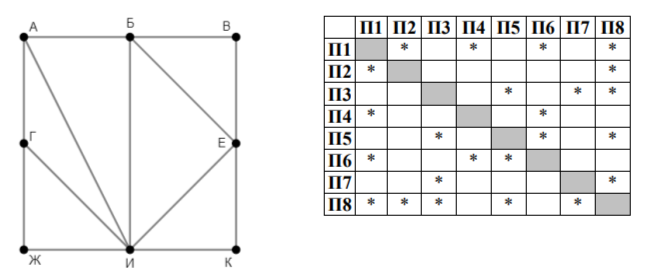
Задание 1. На рисунке схема дорог изображена в виде графа, в таблице звёздочкой отмечено наличие дороги между двумя населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация пунктов в таблице никак не связана с буквенными обозначениями на графе. Кроме того, при заполнении таблицы одну дорогу случайно пропустили. Определите два населённых пункта, дорога между которыми есть на графе, но не отмечена в таблице. В ответе запишите номера этих пунктов в таблице в порядке возрастания, без разделителей между ними, как двузначное число. Например, если бы в таблице была пропущена дорога между пунктами П1 и П2, в ответе следовало бы написать число 12
Задание 2. Логическая функция F задаётся выражением: (x ≡ ¬(w ≡ y)) ∧ (w ≡ (y → z))
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных w, x, y, z.

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть заданы выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу переменная x. В ответе нужно написать: yx.
→ Узнать ответ
Задание 3. В файле приведён фрагмент базы данных «Продукты», содержащей информацию о поставках товаров и их продаже. База данных состоит из трёх таблиц.
Таблица «Торговля» содержит записи о поставках и продажах товаров в магазинах города в июне 2021 г. Таблица «Товар» содержит данные о товарах. Таблица «Магазин» содержит данные о магазинах.

На рисунке приведена схема базы данных, содержащая все поля каждой таблицы и связи между ними. Используя информацию из приведённой базы данных, определите, в магазины какого района Молокозавод №2 поставил с 7 по 9 июня товаров на наибольшую сумму.
В ответе запишите число – найденное значение наибольшей суммы в рублях.
→ Узнать ответ
Задание 4. Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Э – 011, К – 11010, З – 1011, А – 010, М – 1100, Е – 00, Н – 1010
Какое наименьшее количество единиц может содержать код слова ЗАДАЧА?
→ Узнать ответ
Задание 5. Алгоритм получает на вход натуральное число N и строит по нему новое число R следующим образом.
1 Строится двоичная запись числа N.
2 Если в двоичной записи числа N нулей больше, чем единиц, то самый левый ноль заменяется на единицу. В противном случае самая правая единица заменяется на ноль.
3 Результат переводится в десятичную систему счисления.
4 Результатом работы алгоритма становится модуль разности исходного числа N и числа, полученного на предыдущем шаге.
Пример 1 Дано число N = 17 Алгоритм работает следующим образом.
1 Строим двоичную запись числа N: 17_10 = 100012
2 В полученном двоичном числе нулей больше, заменяем самый левый ноль: 10001 → 11001
3 Переводим в десятичную систему: 11001_2 = 25_10
4 Вычисляем модуль разности: | 17 – 25 | = 8
Пример 2 Дано число N = 28 Алгоритм работает следующим образом.
1 Строим двоичную запись числа N: 28_10 = 11100_2
2 В полученном двоичном числе нулей не больше, заменяем самую правую единицу: 11100 → 11000
3 Переводим в десятичную систему: 11000_2 = 24_10
4 Вычисляем модуль разности: | 28 – 24 | = 4
Результат работы алгоритма R = 4
При каком наименьшем N, не превышающем 25·107, в результате работы алгоритма получится наибольшее значение R?
→ Узнать ответ
Задание 6. Исполнитель Чертёжник передвигается по плоскости и оставляет след в виде линии. Чертёжник может выполнять две команды: Точка (x, y) (x и y – числа) и Вектор (a, b) (a и b – числа). По команде Точка (x, y) Чертёжник перемещается в точку с координатами (x, y). По команде Вектор (a, b) Чертёжник смещается на вектор (a, b), то есть переходит из точки с координатами (x, y) в точку с координатами (x + a, y + b).
В начальный момент Чертёжник находится в начале координат.
Чертёжник выполнил следующую программу:
Вектор (5, 1) Вектор (–2, 10) Точка (0, 0)
Определите площадь фигуры, полученной при этом построении. В ответе запишите целую часть числа, полученного при умножении найденной площади на 100
→ Узнать ответ
Задание 7.В информационной системе музея каждый экспонат представлен фотографией и описанием. Фотографии имеют размер 1536×900 пикселей и палитру из 2^24 цветов. При сохранении фотографии сжимаются, их размер уменьшается в среднем на 70%. Известно, что информация о 800 экспонатах занимает в системе 1100 Мбайт. Сколько Кбайт в среднем занимает описание одного экспоната? Ответ округлите до целого числа.
→ Узнать ответ
Задание 8. Сколько существует натуральных чисел, запись которых в системе счисления с основанием 13 содержит не менее двух цифр, и при чтении числа слева направо каждая следующая цифра оказывается строго больше предыдущей?
→ Узнать ответ
Задание 9. В каждой строке электронной таблицы записаны восемь натуральных чисел.
Число в строке считается заметным, если оно строго больше среднего арифметического всех чисел строки. Определите количество строк таблицы, для которых одновременно выполнены следующие условия:
– количество заметных чётных чисел в строке меньше количества заметных нечётных чисел в строке;
– сумма всех чётных чисел строки больше суммы всех нечётных чисел строки.
→ Узнать ответ
Задание 10. Определите, сколько раз в главе 5 повести братьев Стругацких «Трудно быть богом» встречается сочетание букв «из» не как отдельное слово и не как начало слова. Например, «из» в слове «жизнь» надо учитывать, а в словах «из» и «изба» – не надо.
→ Узнать ответ
Задание 11. Для передачи зашифрованных сообщений используется специальный алфавит из 400 символов. Сообщения передаются двоичным кодом, при этом используется равномерное посимвольное кодирование, каждый символ кодируется одинаковым для всех символов минимальным числом бит, а сообщение в целом – минимально возможным числом байт.
При передаче сообщение делится на группы размером не более 9 байт и к каждой такой группе добавляется заголовок из 1 байта.
Суммарный размер сообщения при передаче должен быть не более 1 Кбайт.
Какое наибольшее количество символов может входить в одно сообщение?
→ Узнать ответ
Задание 12. Исполнитель Редактор получает на вход строку цифр и преобразует её.
Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 527150
Если в строке нет вхождений цепочки v, то выполнение команды
заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (111) ИЛИ нашлось(222)
заменить (111, 22)
заменить (222, 11)
заменить (11, 2)
заменить (22, 1)
КОНЕЦ ПОКА
КОНЕЦОпределите, сколько различных строк может получиться в результате применения этой программы к строкам, состоящим только из двоек.
→ Узнать ответ
Задание 13. В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места – нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.
Известно, что для узла 130.0.5.80 количество единиц в двоичной записи адреса сети равно количеству единиц в двоичной записи номера узла в пределах сети.
Какое наибольшее число узлов, адреса которых обладают тем же свойством (включая уже названный), может быть в этой сети?
→ Узнать ответ
Задание 14. В системе счисления с основанием p выполняется равенство zx + xy = zyB.
Буквами x, y, и z обозначены некоторые цифры из алфавита системы счисления с основанием p. Определите значение числа xyzp и запишите это значение в десятичной системе счисления.
→ Узнать ответ
Задание 15. На числовой прямой даны три отрезка: P = [167242; 514210], Q = [403149; 718530], R = [522897; 816282]. Известно, что для некоторого отрезка A логическое выражение (x ∈ Q) → (((x ∈ P) ∨ (x ∈ R)) → (x ∈ A)) истинно (т.е. принимает значение 1) при любом значении переменной x. Определите наименьшее возможное количество целочисленных точек, принадлежащих отрезку A.
→ Узнать ответ
Задание 16. Обозначим через a%b остаток от деления натурального числа a на натуральное число b, а через a//b – целую часть от деления a на b. Функция F(n), где n – неотрицательное целое число, задана следующими соотношениями: F(n) = 0, если n = 0; F(n) = F(n//10) + n%10, если n>0 и n чётно; F(n) = F(n//10), если n нечётно. Сколько существует таких натуральных чисел n, что 4·107 ≤ n ≤ 9·107 и F(n) = 0?
→ Узнать ответ
Задание 17. Файл содержит последовательность натуральных чисел, не превышающих 100 000. Назовём тройкой три идущих подряд элемента последовательности. Определите количество троек, для которых выполняются следующие условия: – в тройке не более одного пятизначного числа; – в тройке есть число, последняя цифра которого совпадает с последней цифрой минимального элемента всей последовательности; – в тройке нет чисел, последняя цифра которых совпадает с последней цифрой максимального элемента всей последовательности. В ответе запишите два числа: сначала количество найденных троек, затем максимальную величину суммы элементов этих троек.
→ Узнать ответ
Задание 18. Робот стоит в левом нижнем углу прямоугольного поля, в каждой клетке которого записано целое число. В некоторых клетках записано число –1, в эти клетки роботу заходить нельзя. Для вашего удобства такие клетки выделены тёмным фоном. В остальных клетках записаны положительные числа. За один ход робот может переместиться на одну клетку вправо или на одну клетку вверх. В начальный момент робот обладает запасом энергии 1000 условных единиц. Расход энергии на запуск робота равен числу, записанному в стартовой клетке. В дальнейшем расход энергии на переход в каждую следующую клетку равен числу, записанному в этой клетке. Если оставшийся у робота запас энергии меньше записанного в клетке числа, робот не может перейти в эту клетку.
Задание 1. Определите максимальное количество шагов, которое может сделать робот.
Задание 2. Определите общее количество клеток поля, включая стартовую, в которые может попасть робот. Исходные данные записаны в электронной таблице. В ответе запишите два числа: сначала ответ на задание 1, затем ответ на задание 2.
→ Узнать ответ
Задание 19. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. Если количество камней в куче делится на целое k, то игрок может добавить в кучу k камней. Например, если в куче 6 камней, то за один ход можно добавить 1, 2, 3 или 6 камней. Игра завершается, когда количество камней в куче становится более 111. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 112 или больше камней. В начале игры в куче было S камней, S < 112. Укажите минимальное значение S, при котором Петя не может выиграть первым ходом, но при любом первом ходе Пети Ваня может выиграть своим первым ходом.
→ Узнать ответ
Задание 20. Для игры, описанной в задании 19, найдите наименьшее и наибольшее значения S, при которых Петя не может выиграть первым ходом, но у Пети есть выигрышная стратегия, позволяющая ему выиграть вторым ходом при любой игре Вани. В ответе запишите найденные значения в порядке возрастания.
→ Узнать ответ
Задание 21. Для игры, описанной в задании 19, найдите минимальное значение S, при котором у Вани есть стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, но у Вани нет стратегии, которая позволила бы ему гарантированно выиграть первым ходом
→ Узнать ответ