Единая городская контрольная работа по Математике 11 класс, профильный уровень. вариант № 956

Официальные материалы задания, ответы по Единой городской контрольной работе “ЕГКР” по Математике 11 класс, профильный уровень, вариант № 956 в формате ЕГЭ проходящая 25 марта 2025 г.

Разбор варианта ЕГКР по Математике 11 класс профильный уровень

→ Скачать полные варианты, задания и решения

Вариант № 956 задания и ответы

Задание 1. Один из углов треугольника равен 40°, а величины двух других относятся как 2:3.
Найдите больший угол этого треугольника. Ответ дайте в градусах.

→ Узнать ответ

Задание 2. Длина вектора а равна 5√3 , угол между векторами а и b равен 60°, а скалярное произведение векторов а и b равно 11√3. Найдите длину вектора b.
→ Узнать ответ

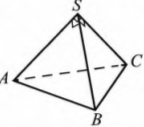
Задание 3. Боковые рёбра треугольной пирамиды взаимно перпендикулярны, длина каждого из них равна 6. Найдите объём пирамиды.

→ Узнать ответ

Задание 4. В пенале у Полины лежали фишки с номерами от 1 до 22. Брат Юра потерял две фишки с чётными номерами. Найдите вероятность того, что случайно взятая Полиной фишка окажется с чётным номером.
→ Узнать ответ

Задание 5. Рекламное агентство использует автоматическую телефонную станцию, которая по введённому списку телефонных номеров дозванивается до абонентов и при ответе передаёт записанное голосовое сообщение. При отсутствии ответа станция набирает номер ещё раз. Если с абонентом не удалось соединиться после пяти попыток, станция набирает номер другого абонента. Установлено, что станция может дозвониться до абонента с первого раза с вероятностью 0,3, а при каждом следующем наборе номера этого абонента вероятность увеличивается на 0,1. Найдите вероятность того, что станция сможет передать абоненту сообщение не позднее третьего набора его номера.
→ Узнать ответ

Задание 6. Найдите корень уравнения √2x+√3=√27
→ Узнать ответ

Задание 7. Найдите значение выражения log2 3 * log9 2.
→ Узнать ответ

Задание 8. На рисунке изображён график у=f ‘(x) производной функции f(x) , определённой на интервале (-3 ;9). Найдите количество точек минимума функции f(x) , принадлежащих отрезку [-2;8,5].

→ Узнать ответ

Задание 9. После дождя уровень воды в колодце повышается. Мальчик измеряет время падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h = 5t2 , где h — расстояние (в метрах), t — время падения (в секундах). До дождя время падения камешков составляло 0,6 секунды. На сколько метров должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 секунды? Ответ дайте в метрах.
→ Узнать ответ

Задание 10. Имеется два сплава. Первый сплав содержит 10% меди, второй — 40 % меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30 % меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
→ Узнать ответ

Задание 11. На рисунке изображён график функции f(х )=ах+b. Найдите значение х, при котором f(х) = 29.

→ Узнать ответ

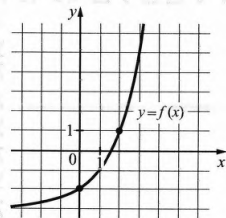
Задание 12. Найдите наибольшее значение функции у=х3-147х+11 на отрезке [-8;0].
→ Узнать ответ