МЦКО по Математике углубленный уровень 10 класс 1 вариант от 29.04.2025

Официальные задания и ответы к МЦКО по Математике углубленный уровень для 10 класса на 29.04.2025 год, вариант № 1 заданий с ответами и решениями.

→ Скачать полные официальные варианты с решениями по Математике угл 10 класс

МЦКО по Математике углубленный уровень 10 класс задания и ответы

Вариант № 1 от 29.04.2025

Задание 1. Найдите значение выражения 2√2 sin 5π/8*cos5π/8/tg3π/10*tgπ/5
→ Узнать ответ

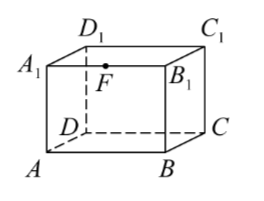
Задание 2. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ точка F – середина ребра A₁B₁, AB = 4, AD = 5, AA₁ = 2 √5 . Найдите тангенс угла между прямыми BC и DF.

→ Узнать ответ

Задание 3. В графе 30 рёбер. Каждая вершина графа имеет или степень 2, или степень 7. Причём вершин степени 2 в четыре раза меньше, чем вершин степени 7. Сколько вершин в этом графе?
→ Узнать ответ

Задание 4. Укажите, какое из утверждений верно. Любые две плоскости имеют общую прямую, на которой лежат все общие точки этих плоскостей. Для любых двух скрещивающихся прямых существует плоскость, которая проходит через одну из них и параллельна другой. Если плоскость параллельна одной из двух перпендикулярных прямых, то она перпендикулярна второй прямой.
→ Узнать ответ

Задание 5. Найдите количество элементов множества A ∩ (B ∩ C), где
A – множество двузначных натуральных чисел,
B – множество чисел, кратных числу 23,
C – множество чисел, которые представимы в виде 17n + 1, где n ∈ ℤ.
→ Узнать ответ

Задание 6. Решите уравнение  2 log ₄ (x² – 4) – log _0,5 x – 2/x + 2=-4
Если уравнение имеет больше одного корня, в ответ запишите сумму всех его корней.
→ Узнать ответ

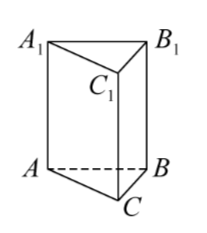
Задание 7. В правильной треугольной призме ABCA₁B₁C₁ найдите расстояние от точки A₁ до плоскости AB₁C₁, если AB = 4, AA₁ = 6.

→ Узнать ответ

Задание 8. Решите уравнение 16 ^{x 2 – 1} – 65 ∙ 2 ^{2 x 2 – 5} + 1 = 0. Если уравнение имеет больше одного корня, в ответ запишите произведение корней.
→ Узнать ответ

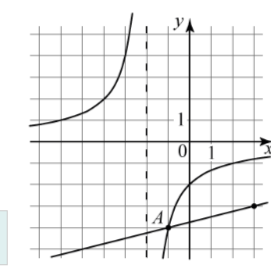
Задание 9. На рисунке изображены графики функций f(x) = k и g(x) = px + b, x – a которые пересекаются в точках A(–1; – 4) и B(xB ; yB ). Найдите xB .

→ Узнать ответ

Задание 10. Стрелок при стрельбе попадает в большую мишень с вероятностью 0,4, а в мелкую – с вероятностью 0,2. Во сколько раз вероятность попасть одним выстрелом по большой мишени меньше вероятности попасть хотя бы один раз тремя выстрелами по мелкой мишени?
→ Узнать ответ

Задание 11. Решите неравенство x ³ – 7 x ² + 11 x + 3/8 – x≥ 0
В ответ запишите количество целых решений неравенства на отрезке [– 60; 60].
→ Узнать ответ

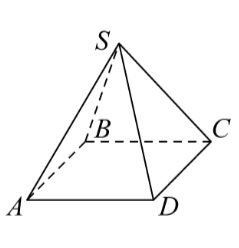
Задание 12. В правильной пирамиде SABCD с вершиной S ребро основания равно 6, а боковое ребро равно 7. Найдите косинус угла между плоскостями BSC и CSD.

→ Узнать ответ