МЦКО по Математике углубленный уровень 10 класс 2 вариант от 29.04.2025

Официальные задания и ответы к МЦКО по Математике углубленный уровень для 10 класса на 29.04.2025 год, вариант № 2 заданий с ответами и решениями.

→ Скачать полные официальные варианты с решениями по Математике угл 10 класс

МЦКО по Математике углубленный уровень 10 класс задания и ответы

Вариант № 2 от 29.04.2025

Задание 1. Найдите значение выражения 3tg 3π/10*tgπ/5/sin5π/12*cos5π/12
→ Узнать ответ

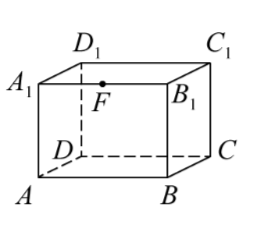
Задание 2. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ точка F – середина ребра A₁B₁, AB = 8, AD = 4, AA₁ = 2 √5 . Найдите тангенс угла между прямыми BC и DF.

→ Узнать ответ

Задание 3. В графе 64 ребра. Каждая вершина графа имеет или степень 5, или степень 9. Причём вершин степени 5 в три раза меньше, чем вершин степени 9. Сколько вершин в этом графе?
→ Узнать ответ

Задание 4. Укажите, какое из утверждений верно.
Если прямая b в пространстве пересекает прямую a, то она пересекает и любую другую прямую, параллельную прямой a
Любая плоскость, пересекающаяся с одной из параллельных прямых, пересекается и с другой прямой.
Если прямая параллельна одной из двух перпендикулярных плоскостей, то она имеет хотя бы одну общую точку со второй плоскостью.
→ Узнать ответ

Задание 5. Найдите количество элементов множества A ∩ (B ∩ C), где
A – множество двузначных натуральных чисел,
B – множество чисел, кратных числу 23,
C – множество чисел, которые представимы в виде 17n + 1, где n ∈ ℤ.
→ Узнать ответ

Задание 6. Решите уравнение  2 log ₄ (x² – 4) – log _0,5 x + 2/x — 2=-2
Если уравнение имеет больше одного корня, в ответ запишите сумму всех его корней.
→ Узнать ответ

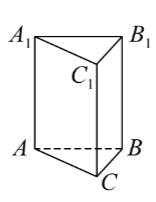
Задание 7. В правильной треугольной призме ABCA₁B₁C₁ найдите расстояние от точки A до плоскости A₁BC, если AB = 2, AA₁ = 3.

→ Узнать ответ

Задание 8. Решите уравнение 2 ^{x 2 – 4} – 33 ∙ 2 ^{0,5 x 2 – 4,5} + 1 = 0.
Если уравнение имеет больше одного корня, в ответ запишите произведение корней.
→ Узнать ответ

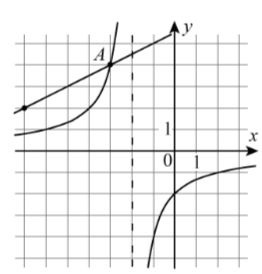
Задание 9. На рисунке изображены графики функций f(x) = k и g(x) = px + b, x – a которые пересекаются в точках A(–3; 4) и B(xB ; yB ). Найдите xB .

→ Узнать ответ

Задание 10. Стрелок при стрельбе попадает в большую мишень с вероятностью 0,5, а в мелкую – с вероятностью 0,1. Во сколько раз вероятность попасть хотя бы один раз двумя выстрелами по большой мишени меньше вероятности не попасть ни разу, стреляя два раза по мелкой мишени?
→ Узнать ответ

Задание 11. Решите неравенство x 3 – 5 x 2 – 3 x + 3/14 – x≥ 0
В ответ запишите количество целых решений неравенства на отрезке [– 60; 60].
→ Узнать ответ

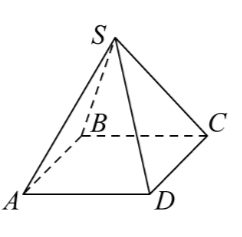
Задание 12. В правильной пирамиде SABCD с вершиной S ребро основания равно 4, а боковое ребро равно 3. Найдите косинус угла между плоскостями ASB и BSC.

→ Узнать ответ