Официальные задания и ответы к демоверсии МЦКО по Математике (Углубленный уровень) для 10 класса на апрель-май 2025 г., содержит 1 (один) тренировочный вариант заданий с ответами и решениями. Данный материал разработан для подготовки к диагностическому тестированию в общеобразовательных учреждениях Москвы.
→ Скачать официальные варианты по МЦКО 2024-2025
Подготовка к диагностике МЦКО по Математике (Углубленный уровень) 10 класс: демоверсия 2025 г.
Проверочная работа проводится с целью осуществления мониторинга уровня и качества подготовки обучающихся в порядке, принятом Департаментом образования и науки города Москвы. Назначение проверочной работы по учебному предмету «Математике (Углубленный уровень)» – оценить качество общеобразовательной подготовки обучающихся 10 классов в соответствии с требованиями федерального государственного образовательного стандарта основного общего образования и федеральной образовательной программы основного общего образования. Период проведения – апрель–май 2025 года.
Время выполнения диагностической работы
Время выполнения проверочной работы – 70 минут без учёта времени на перерыв для разминки глаз. В работе предусмотрен один автоматический пятиминутный перерыв.
Условия проведения диагностической работы
При организации и проведении работы необходимо строгое соблюдение порядка организации и проведения независимой диагностики. Проверочная работа проводится в компьютерной форме. Дополнительные материалы и оборудование не используются.
Официальная демонстрационная версия МЦКО для 10 класса: задания и ответы
Задание 1. Найдите значение выражения 12sin75*cos75*cos25/sin(-115)
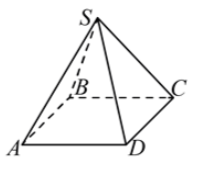
Задание 2. В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 18, а боковое ребро AS равно 15. Найдите синус угла между прямыми AB и SD.
Задание 3. Укажите номера всех графов, в которых существует эйлеров путь, то есть путь, соединяющий все вершины графа и проходящий через каждое ребро ровно по одному разу.
 |  |  |  |
Задание 4. Какое из утверждений неверно?
Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
Через любую точку пространства проходит бесконечно много прямых, перпендикулярных данной прямой.
Если плоскость перпендикулярна одной из двух перпендикулярных плоскостей, то она параллельна другой плоскости.
Задание 5. Найдите количество элементов множества (B◡C)◠A, где
A – множество двузначных натуральных чисел,
B – множество чисел, не кратных числу 3,
C – множество чисел, кратных числу 4.
Задание 6. Решите уравнение log_4(2-x)^3+4log_8(2-x)=8,5. Если уравнение имеет больше одного корня, в ответ запишите сумму всех его корней.
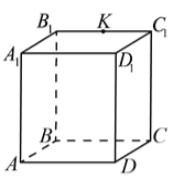
Задание 7. В прямоугольном параллелепипеде ABCDA1B1C1D1 точка K – середина ребра B1C1, AB = 11, AD = 4√11, AA1 = 3√22. Найдите расстояние от точки A1 до плоскости CDK.
Задание 8. Решите уравнение 4*9^x+0,5+9*4^x+0,5=35*6^x. Если уравнение имеет больше одного корня, в ответ запишите сумму корней.
Задание 9. На рисунке изображены графики функций f(x)=a√x+c+d и g(x)=kx+b, которые пересекаются в точках A(0;2) и B (X_B;Y_B). Найдите X_B
Задание 10. На одной полке стоит 36 блюдец: 14 синих и 22 красных. На другой полке стоит 36 чашек: 27 синих и 9 красных. Наугад берут два блюдца и две чашки. Найдите вероятность, что из них можно будет составить две чайные пары (блюдце с чашкой), каждая из которых будет одного цвета.
Задание 11. Решите неравенство 2x^3-21x^2+36x+108/4-x =>0. В ответ запишите количество целых решений неравенства на отрезке [-100;100]
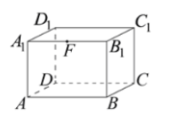
Задание 12. В прямоугольном параллелепипеде ABCDA1B1C1D1 точка F – середина ребра A1B1, AA1 = 12, AD = 10, AB = 15. Найдите тангенс угла между плоскостями BFC1 и ABC.