
Официальные задания и ответы к демоверсии МЦКО по Математике для 10 класса на 29.04.2025 год, содержит 1 (один) тренировочный вариант заданий с ответами и решениями. Данный материал разработан для подготовки к диагностическому тестированию в общеобразовательных учреждениях Москвы.
→ Скачать официальные варианты по МЦКО 2024-2025
Подготовка к диагностике МЦКО по Математике 10 класс: демоверсия 2025 г.
Проверочная работа проводится с целью осуществления мониторинга уровня и качества подготовки обучающихся в порядке, принятом Департаментом образования и науки города Москвы. Назначение проверочной работы по учебному предмету «Математике» – оценить качество общеобразовательной подготовки обучающихся 10 классов в соответствии с требованиями федерального государственного образовательного стандарта основного общего образования и федеральной образовательной программы основного общего образования.
Период проведения – апрель–май 2025 года.
Время выполнения диагностической работы
Время выполнения проверочной работы – 90 минут без учёта времени на перерыв для разминки глаз. В работе предусмотрен один автоматический пятиминутный перерыв.
Условия проведения диагностической работы
При организации и проведении работы необходимо строгое соблюдение порядка организации и проведения независимой диагностики. Проверочная работа проводится в компьютерной форме. Дополнительные материалы и оборудование не используются.
Официальная демонстрационная версия МЦКО для 10 класса: задания и ответы
Задание 1. В некотором городе 40 % населения интересуется футболом. Остальные горожане футболом не интересуются и футбольные матчи не смотрят. Среди тех, кто интересуется футболом, финальный матч чемпионата России смотрели 70 %. Сколько процентов горожан смотрели финальный матч?
Задание 2. Найдите значение выражения a^-8/3 * a^5/a^2 при a=64
Задание 3. Вычислите: cos (-60)+sin^2 45
Задание 4. Найдите сумму бесконечно убывающей геометрической прогрессии 16, 8, 4, 2, 1, 1/2
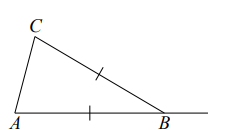
Задание 5. Известно, что в треугольнике ABC стороны AB и BC равны. Внешний угол при вершине B равен 138 . Найдите угол C. Ответ дайте в градусах.
Задание 6. Из коробки, в которой лежат 15 чёрных и 5 красных маркеров, достают один случайный маркер. Найдите вероятность того, что он окажется красным.
Задание 7. Каждый из 25 учащихся в классе посещает хотя бы один из двух кружков. Известно, что 10 человек занимаются в химическом кружке, а 18 в биологическом. Сколько учащихся посещают оба кружка?
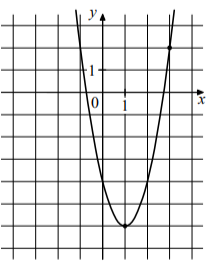
Задание 8. На рисунке изображён график функции f(x)=ax^2-4x+c.Найдите f(-3)
Задание 9. Симметричный игральный кубик бросили два раза. Известно, что при первом броске выпало больше очков, чем при втором. Какова вероятность того, что в сумме выпало семь очков?
Задание 10. Найдите tga, если sina=0.8 и π/2<a<π
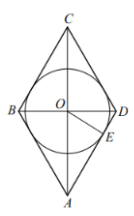
Задание 11. В ромбе ABCD диагонали пересекаются в точке О. Окружность радиусом 4 вписана в ромб и касается стороны AD в точке Е. Найдите площадь ромба, если известно, что DE = 2.
Задание 12. Дана четырёхугольная пирамида SABCD с вершиной S. Основание ABCD является прямоугольной трапецией с прямыми углами A и D. Отрезок SD перпендикулярен плоскости основания. Выберите из предложенного списка пары перпендикулярных прямых.
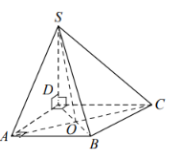
1) прямые SA и АВ
2) прямые SA и DB
3) прямые AB и SC
4) прямые SD и CB
Задание 13. Решите уравнение cos^2=cosx.
Запишите в ответ количество корней этого уравнения, принадлежащие отрезку [5; 15].
Задание 14. Решите неравенство 3x^2-2x-1/5x+1 <= 0
В ответ запишите наибольшее целое отрицательное число полученного решения.
Задание 15. Построив график функция f(x)=||x|-3|+2, найдите с, при котором уравнение f(x)=c имеет три различных корня.
Задание 16. Дана треугольная пирамида SABC с вершиной в точке S. Треугольник ABC равносторонний с центром точке O. Отрезок SO перпендикулярен плоскости основания. Известно, что AB = 6, а sa=4√3.Найдите расстояние от точки S до плоскости ABC
Задание 17. Баскетболист два раза бросает мяч в кольцо. При первом броске вероятность попадания равна 0,4. Если баскетболист промахнулся при первом броске, то при втором броске вероятность попадания не меняется, а если попал в кольцо, то при втором броске вероятность попадания равна 0,7. Какова вероятность того, что баскетболист попадёт мячом в кольцо ровно один раз?