Официальные задания и ответы к демоверсии МЦКО по Математике для 7 класса на 21-24.04.2025 год, содержит 1 (один) тренировочный вариант заданий с ответами и решениями. Данный материал разработан для подготовки к диагностическому тестированию в общеобразовательных учреждениях Москвы.
→ Скачать официальные варианты по МЦКО 2024-2025
Подготовка к диагностике МЦКО по Математике 7 класс: демоверсия 2025 г.
Проверочная работа проводится с целью осуществления мониторинга уровня и качества подготовки обучающихся в порядке, принятом Департаментом образования и науки города Москвы. Назначение проверочной работы по учебному предмету «Математика» – оценить качество общеобразовательной подготовки обучающихся 7 классов в соответствии с требованиями федерального государственного образовательного стандарта основного общего образования и федеральной образовательной программы основного общего образования. Период проведения – апрель–май 2025 года.
Время выполнения диагностической работы
Время выполнения каждой части проверочной работы (часть 1, часть 2) – 45 минут без учёта времени на перерыв для разминки глаз. В работе предусмотрен один автоматический пятиминутный перерыв.
Условия проведения диагностической работы
При организации и проведении работы необходимо строгое соблюдение порядка организации и проведения независимой диагностики. Проверочная работа проводится в компьютерной форме. Дополнительные материалы и оборудование: линейка.
Официальная демонстрационная версия МЦКО для 7 класса: задания и ответы
Задание 1. Найдите значение выражения 5/6+7/12/7/2
Задание 1. Найдите значение выражения 2,6-8,4/2,5
Задание 2. Трактор едет по дороге, проезжая 10 метров за каждую секунду. Выразите скорость трактора в километрах в час.
Задание 3. Найдите корень уравнения 2(4+3x)=-x-13.
Задание 4. Отметьте на числовой прямой точку A (-2 6/7)

Задание 5. Из пункта А в направлении пункта Б, расстояние между которыми равно 240 км, в 7 часов утра выехал велосипедист, а через некоторое время из пункта А в том же направлении выехал автомобиль. Доехав до пункта Б, автомобиль сделал остановку на 3 часа, а затем с той же скоростью поехал обратно. На рисунке график движения велосипедиста обозначен цифрой 1, график движения автомобиля обозначен цифрой 2 и приведён не полностью.
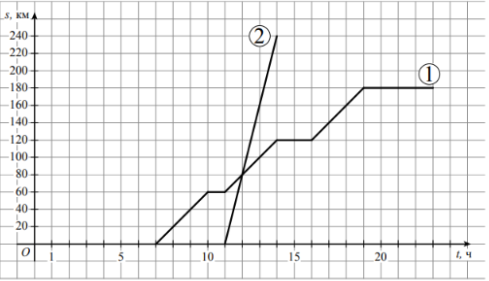
Найдите, на каком расстоянии от пункта А автомобиль догнал велосипедиста. Ответ дайте в километрах.
На том же рисунке достройте график движения автомобиля до момента возвращения в пункт А.
Задание 6. Найдите значение выражения (4-y)^2-y(y+1) при y=-1/9
Задание 7. Решите систему уравнений { 5x+2y=2 , 2x-y=-10
Задание 8. Хоккейные коньки в апреле стоили 4500 руб. В мае цену снизили на 20 %. В октябре цену повысили на 10 %. Сколько рублей стали стоить коньки?
Задание 9. На первом участке собрали по 420 тонн огурцов с каждого гектара; на втором – по 360 тонн, а на третьем – по 520 тонн. Площадь первого участка равна 20; второго – 55; третьего – 25 гектаров. Сколько тонн огурцов собрали в среднем с одного гектара на всех трёх участках?
Задание 10. Задумали трёхзначное число, последняя цифра которого не равна нулю. Из него вычли трёхзначное число, записанное теми же цифрами в обратном порядке. Получили число 792.
Найдите наименьшее число, обладающее таким свойством.
Задание 11. На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C . Найдите расстояние от точки A до прямой BC .
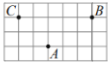
Задание 12. В треугольнике ABC угол BAC равен 40° , АC=CB. Найдите внешний угол при вершине C .
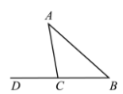
Задание 13. Параллельные прямые AB и CD пересекают прямую EF в точках K и M соответственно. Угол FMD равен 28° . Найдите угол AKM. Ответ дайте в градусах
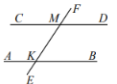
Задание 14. В треугольнике ABC проведена биссектриса CE . Найдите величину угла BCE , если ∠BAC=46 и ∠ABC=78.
Задание 14. В треугольнике АВС на стороне АС отметили произвольную точку М . В треугольнике ABM провели биссектрису MK . В треугольнике СВМ построили высоту МР . Угол KMP равен 90° , CM =12 . Найдите ВM .
Задание 15. Укажите верное утверждение.
Один из смежных углов всегда тупой.
Любая высота равнобедренного треугольника совпадает с его медианой.
Если угол прямоугольного треугольника равен 60°, то его гипотенуза в два раза больше одного из катетов.
Задание 16. Таблица содержит данные о росте учащихся класса.
| Фамилия | Рост, см | Фамилия | Рост, см | Фамилия | Рост, см |
|---|---|---|---|---|---|
| Алексеев | 156 | Гетманов | 160 | Завидов | 163 |
| Андреева | 159 | Дубова | 156 | Коваль | 154 |
| Борисов | 162 | Евсеева | 1154 | Петровская | 149 |
| Вольский | 158 | Железов | 167 | Юсуфов | 165 |
Найдите явно ошибочное значение (выброс), внесённое в эту таблицу.
Из данных о росте учащихся удалите выброс и найдите размах оставшихся значений.
Задание 17. Катя младше Тани, но старше Даши. Ксюша не младше Даши. Укажите все верные утверждения.
Таня и Даша одного возраста.
Среди указанных девочек нет никого младше Даши.
Таня старше Даши.
Таня и Катя одного возраста.
Задание 18. На рисунке показан абажур, изготовленный из стальной проволоки. Какое наименьшее количество кусков проволоки нужно, чтобы изготовить абажур, показанный на рисунке?