
Официальные задания и ответы к демоверсии МЦКО по Математике Базовый уровень для 8 класса на 25-30.04.2025 год, содержит 1 (один) тренировочный вариант заданий с ответами и решениями. Данный материал разработан для подготовки к диагностическому тестированию в общеобразовательных учреждениях Москвы.
→ Скачать официальные варианты по МЦКО 2024-2025
Подготовка к диагностике МЦКО по Математике 8 класс: демоверсия 2025 г.
Проверочная работа проводится с целью осуществления мониторинга уровня и качества подготовки обучающихся в порядке, принятом Департаментом образования и науки города Москвы. Назначение проверочной работы по учебному предмету «Математика» – оценить качество общеобразовательной подготовки обучающихся 8 классов в соответствии с требованиями федерального государственного образовательного стандарта основного общего образования и федеральной образовательной программы основного общего образования. Период проведения – апрель–май 2025 года.
Время выполнения диагностической работы
Время выполнения каждой части проверочной работы (часть 1, часть 2) – 45 минут без учёта времени на перерыв для разминки глаз. В работе предусмотрен один автоматический пятиминутный перерыв.
Условия проведения диагностической работы
При организации и проведении работы необходимо строгое соблюдение порядка организации и проведения независимой диагностики. Проверочная работа проводится в компьютерной форме. Дополнительные материалы и оборудование: линейка.
Официальная демонстрационная версия МЦКО для 8 класса: задания и ответы
Задание 1. Найдите значение выражения 4,5*5,4-6,1.
Задание 2. Найдите больший корень уравнения (5x-2)(3-x) = 0.
Задание 3. Одно число больше другого на 22, а их произведение равно -120. Найдите меньшее из этих чисел.
Задание 4. На числовой прямой отмечены числа a и b . Отметьте на прямой какую-нибудь точку x так, чтобы при этом выполнялись три условия: x-a>0 , x-b<0 и a^2*x>0 .
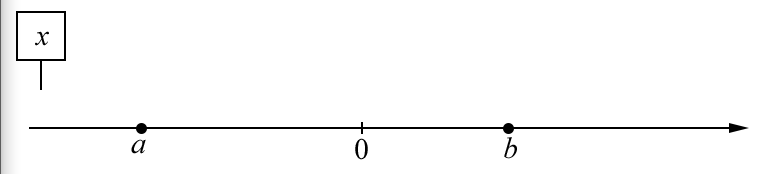
Задание 5. Установите соответствие между графиками функций и формулами, которые задают эти функции.
ГРАФИКИ
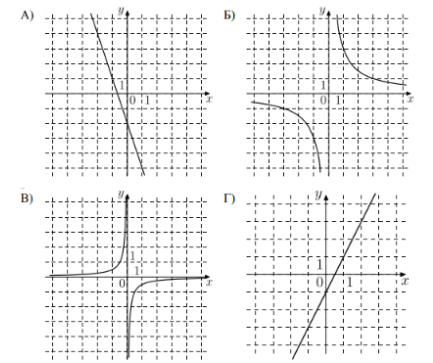
ФОРМУЛЫ
1) y=2x-1
2) y-3x-2
3) y=3/4
4) y=-1/2x
Задание 6. Отметьте на числовой прямой число √34

Задание 7. Найдите значение выражения xy+y^2/8x*4x/x+y при x=√3. y=-5.2
Задание 8. Найдите меньший корень уравнения 4×2+12x+9=(x–4)2.
Задание 9. Расстояние между пунктами А и В по реке равно 45 км. Из пункта А в пункт В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в пункт А. К моменту возвращения лодки в пункт А плот проплыл 32 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
Задание 10. Найдите значение выражения √7-4√3+√3
Задание 11. Один из углов параллелограмма равен 70° . Найдите тупой угол данного параллелограмма.
Задание 12. В треугольнике ABC известны стороны: AB = 25, AC = 40 , BC = 25 . Найдите площадь треугольника ABC .
Задание 13. Укажите утверждение, которое является истинным высказыванием.
Любой параллелограмм, в котором две стороны равны, является ромбом.
Любой четырёхугольник, в котором две диагонали равны и перпендикулярны, является квадратом.
Любой параллелограмм, в котором диагонали равны, является прямоугольником.
В любой трапеции оба угла при меньшем основании тупые.
Задание 14. В прямоугольном треугольнике ABC с гипотенузой AB провели высоту CD и биссектрису CL. Найдите величину угла DCL, если ∠CAB = 25°. Ответ дайте в градусах.
Задание 15. На фестивале выступают группы из 15 разных городов: по одной из каждого города. Среди этих городов есть Астрахань, Брянск и Волгоград. Порядок выступления определяется жребием. Какова вероятность того, что группа из Астрахани будет выступать раньше группы из Брянска, но позже группы из Волгограда?
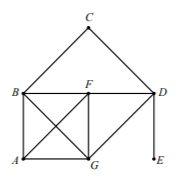
Задание 16. На рисунке изображён граф. Аня обвела этот граф, не отрывая карандаша от листа бумаги и не проводя ни по одному ребру дважды. С какой вершины Аня начала обводить граф, если она закончила его обводить в вершине E?
Задание 17. На диаграмме представлены данные о годовом количестве осадков в Москве. По горизонтали указаны годы, а по вертикали – количество осадков, в мм.
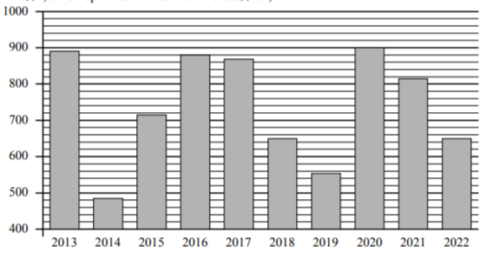
1) В какие годы из указанного периода в Москве за год выпало менее 600 мм осадков?
| 2013 | 2014 | 2015 | 2016 | 2017 |
| 2018 | 2019 | 2020 | 2021 | 2022 |
2) Примерно на сколько мм в 2021 году выпало осадков больше, чем в 2022?
Задание 18. Правильный игральный кубик бросают два раза. Найдите вероятность того, что сумма выпавших очков окажется не меньше 9.