
Официальные задания и ответы к демоверсии МЦКО по Математике углублённый уровень для 7 класса на 21-24.04.2025 год, содержит 1 (один) тренировочный вариант заданий с ответами и решениями. Данный материал разработан для подготовки к диагностическому тестированию в общеобразовательных учреждениях Москвы.
→ Скачать официальные варианты по МЦКО 2024-2025
Подготовка к диагностике МЦКО по Математике Углубленный 7 класс: демоверсия 2025 г.
Проверочная работа проводится с целью осуществления мониторинга уровня и качества подготовки обучающихся в порядке, принятом Департаментом образования и науки города Москвы. Назначение проверочной работы по учебному предмету «Математика» – оценить качество общеобразовательной подготовки обучающихся 7 классов в соответствии с требованиями федерального государственного образовательного стандарта основного общего образования и федеральной образовательной программы основного общего образования. Период проведения – апрель–май 2025 года.
Время выполнения диагностической работы
Время выполнения каждой части проверочной работы (часть 1, часть 2) – 45 минут без учёта времени на перерыв для разминки глаз. В работе предусмотрен один автоматический пятиминутный перерыв.
Условия проведения диагностической работы
ри организации и проведении работы необходимо строгое соблюдение порядка организации и проведения независимой диагностики. Проверочная работа проводится в компьютерной форме. Дополнительные материалы и оборудование: линейка.
Официальная демонстрационная версия МЦКО для 7 класса: задания и ответы
Задание 1. Вычислите: 6^4/4^2*9^3
Задание 2. Найдите значение выражения 112,6^2-6,4^2/4,3^2+2*4,3*1.7+1,7^2
Задание 3. Представьте выражение в виде многочлена стандартного вида: (3-2y)^2-2y(y+1) в виде многочлена стандартного вида. Запишите коэффициенты полученного многочлена (с нужным знаком «+» или «–»)
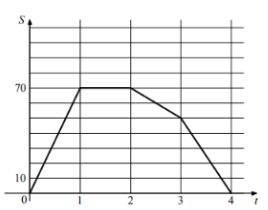
Задание 4. Населённые пункты А и Б соединены прямым шоссе. Автомобиль выехал из пункта А в пункт Б, некоторое время провёл в пункте Б, а затем вернулся в пункт А. График показывает расстояние от автомобиля до пункта А в каждый момент времени. Расстояние измеряется в километрах, время – в часах. Найдите среднюю скорость автомобиля на обратном пути (в км/ч).
Задание 5. Найдите наибольшее шестизначное число, которое делится на 15 и у которого все цифры расположены в порядке убывания (каждая следующая цифра меньше предыдущей, например, 876431).
Задание 6. В классе некоторые ученики простудились и не ходят в школу. В понедельник тех, кто пришёл в школу, было в 13 раз больше, чем тех, кто не пришёл. Во вторник заболели ещё двое, и в результате тех, кто не пришёл в школу, оказалось в 6 раз меньше, чем тех, кто пришёл. Сколько учеников в этом классе?
Задание 7. Решите уравнение 4x(x+2)+3=4x^2-3(7-2x)
Задание 8. Задумали трёхзначное число, последняя цифра которого не равна нулю. Из него вычли трёхзначное число, записанное теми же цифрами в обратном порядке. Получили число 792. Найдите все числа, обладающие таким свойством.
Задание 9. В растворе кислоты на 1 кг воды приходилось 4 кг кислоты. В этот раствор долили воду, так что содержание кислоты понизилось до 20 %. Затем в раствор долили кислоту, и содержание кислоты выросло до 80 %. Во сколько раз увеличилась масса раствора по сравнению с первоначальной?
Задание 10. Угол B треугольника ABC равен 62° . Внешний угол при вершине A равен 138° . Найдите градусную меру внешнего угла при вершине C .
Задание 11. Укажите все верные утверждения.
Существует равнобедренный треугольник, в котором один из углов в 2 раза больше другого.
В любом прямоугольном треугольнике один из катетов в 2 раза меньше другого.
При пересечении двух любых прямых сумма пары образованных ими вертикальных углов равна 180°.
В любом треугольнике длина одной стороны меньше суммы длин двух других сторон.
Задание 12. В треугольнике ABC проведены медиана BM и высота BH. Известно, что AH = 54, BC = BM. Найдите длину стороны AC.
Задание 13. Даны треугольники ABC и ADC, причём точки B и D лежат по разные стороны от прямой AC. Углы ABC и ADC равны 77° и 74° соответственно. Найдите градусную меру угла BAD, если AB = AC = AD.
Задание 14. Катя младше Тани, но старше Даши. Ксюша не младше Даши.
Укажите номера истинных утверждений.
Таня и Даша одного возраста.
Среди указанных девочек нет никого младше Даши.
Таня старше Даши.
Таня и Катя одного возраста.
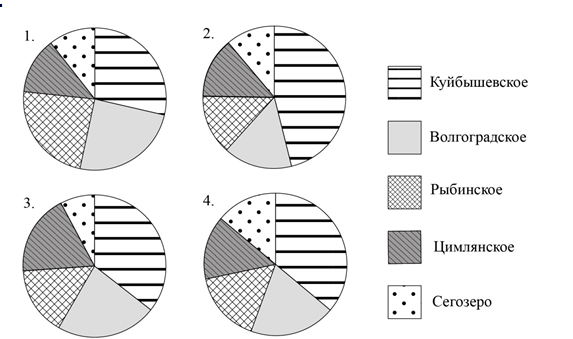
Задание 15. Объём воды в крупных водоёмах измеряют в кубических километрах (1 км3 = 1 млрд м3). В таблице указаны некоторые описательные характеристики объёмов пяти крупнейших водохранилищ Европейской части России: Волгоградского, Куйбышевского, Сегозера, Цимлянского и Рыбинского. Ниже даны четыре диаграммы, показывающие долю каждого водохранилища в их общем объёме. Только одна из диаграмм верная.
| Объём воды, км3 | |
|---|---|
| Среднее арифметическое | 32 |
| Медиана | 25 |
| Максимум | 57 |
| Минимум | 23 |
Укажите номер верной диаграммы.
Найдите примерный объём Волгоградского водохранилища (в км3).
Задание 16. У графа семь вершин степени 4 и ещё шесть вершин степени 3. Других вершин в этом графе нет. Сколько рёбер в этом графе?
Задание 17. В институте используется десятибалльная система оценки знаний студентов. Средняя оценка вычисляется как среднее арифметическое. Преподаватель дал одну и ту же контрольную работу в двух группах. Результаты представлены в таблице.
| Группа | 1 | 2 |
|---|---|---|
| Число студентов | 20 | 30 |
| Средняя оценка | 8,2 | 7,8 |
Найдите среднюю оценку всех студентов за эту работу.
Несколько студентов переписали работу, и каждый получил на 1 балл больше, чем при первой попытке. В результате средняя оценка всех студентов стала равной 8.
Сколько студентов переписало работу?