
Официальные задания и ответы к демоверсии МЦКО по Математике Углубленный уровень для 8 класса на 25-30.04.2025 год, содержит 1 (один) тренировочный вариант заданий с ответами и решениями. Данный материал разработан для подготовки к диагностическому тестированию в общеобразовательных учреждениях Москвы.
→ Скачать официальные варианты по МЦКО 2024-2025
Подготовка к диагностике МЦКО по Математике 8 класс: демоверсия 2025 г.
Проверочная работа проводится с целью осуществления мониторинга уровня и качества подготовки обучающихся в порядке, принятом Департаментом образования и науки города Москвы. Назначение проверочной работы по учебному предмету «Математика» – оценить качество общеобразовательной подготовки обучающихся 8 классов в соответствии с требованиями федерального государственного образовательного стандарта основного общего образования и федеральной образовательной программы основного общего образования. Период проведения – апрель–май 2025 года.
Время выполнения диагностической работы
Время выполнения каждой части проверочной работы (часть 1, часть 2) – 45 минут без учёта времени на перерыв для разминки глаз. В работе предусмотрен один автоматический пятиминутный перерыв.
Условия проведения диагностической работы
При организации и проведении работы необходимо строгое соблюдение порядка организации и проведения независимой диагностики. Проверочная работа проводится в компьютерной форме. Дополнительные материалы и оборудование: линейка.
Официальная демонстрационная версия МЦКО для 8 класса: задания и ответы
Задание 1. Найдите значение выражения √32*√6/√12
Задание 2. Решите уравнение x2-36=5x. Если уравнение имеет более одного корня, запишите в ответ меньший из них.
Задание 3. На числовой прямой отмечены числа a и b . Отметьте на прямой какую-нибудь точку x так, чтобы при этом выполнялись три условия: x-a>0, x-b<0 и a^2x>0
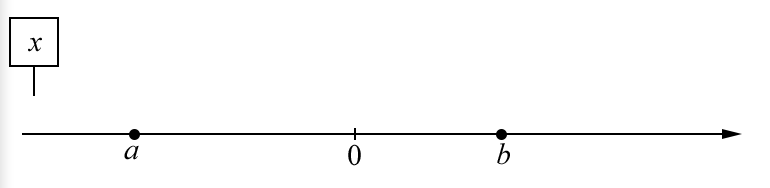
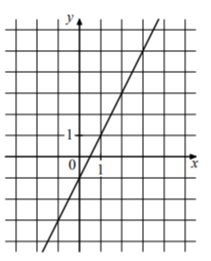
Задание 4. На рисунке изображён график линейной функции. Напишите формулу, которая задаёт эту линейную функцию.
Задание 5. Найдите значение выражения 2x/x-4 – 2x^2-32/x^2-8x+16 при x=3.96
Задание 6. Число A является суммой квадратов трёх последовательных натуральных чисел. Найдите остаток от деления числа A на 3.
Задание 7. Решите неравенство 2x-3/5-4x-7/15 > 8x-7/3. В ответ запишите наибольшее целое число найденного решения.
Задание 8. Решите уравнение (X-3)^4-4(X-3)^2-5=0
Задание 9. Расстояние между пунктами А и В по реке равно 11 км. Из пункта А в пункт В одновременно отправились плот и моторная лодка. Моторная лодка, прибыв в пункт В, тотчас повернула обратно. В двух километрах от пункта А лодка встретила плот. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч. Ответ дайте в км/ч.
Задание 10. Укажите утверждение, которое является истинным высказыванием.
Любой параллелограмм, в котором две стороны равны, является ромбом.
Любой четырёхугольник, в котором две диагонали равны и перпендикулярны, является квадратом.
Любой параллелограмм, в котором диагонали равны, является прямоугольником.
В любой трапеции оба угла при меньшем основании тупые.
Задание 11. В ромбе KLMN диагонали пересекаются в точке T. Из точки T опущен перпендикуляр TH на сторону KN. Найдите тупой угол ромба, если ∠ LTH = 153°. Ответ дайте в градусах.
Задание 12. Боковая сторона равнобедренного треугольника ABC равна 3, а основание AC равно 2. В этом треугольнике провели биссектрисы AL и CM. Найдите длину отрезка LM.
Задание 13. Боковые стороны AB и CD прямоугольной трапеции ABCD равны соответственно 40 и 41. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Задание 14. При формировании продуктового заказа сборщик кладёт в пакет примерно 3 кг картофеля. Расположите следующие события в порядке возрастания их вероятностей.
1) «Масса картофеля в пакете составляет от 2,9 до 3,2 кг».
2) «Масса картофеля в пакете отклоняется от 3 кг не более чем на 100 г».
3) «Масса картофеля в пакете отклоняется от 3 кг не более чем на 200 г».
4) «Масса картофеля в пакете составляет от 2,5 до 3,5 кг».
Задание 15. В графе 14 рёбер. Каждая вершина графа имеет или степень 2, или степень 5. Причём вершин степени 2 столько же, сколько вершин степени 5. Сколько вершин в этом графе?
Задание 16. Правильный игральный кубик бросают два раза. Найдите вероятность того, что сумма выпавших очков окажется не меньше 9.
Задание 17. На день рождения к Паше пришли две Маши и два Саши. Все пятеро расселись за круглым столом. Найдите вероятность того, что Паша сидит между двумя тёзками.