Тренировочная работа СтатГрад №4 по Математике для 11 класса, вариант № МА2410408 задания, ответы — это уникальный материал для подготовки к ЕГЭ, разработанный в соответствии с требованиями ФИПИ и форматом реального экзамена.
Тренировочная работа СтатГрад №4 по Математике для 11 класса
→ Скачать все варианты и решения по Математике 11 класс
Вариант МА2410408 задания и ответы для подготовки к ЕГЭ по Математике
Задание 1. В мужском общежитии института в каждой комнате можно поселить не более трёх человек. Какое наименьшее количество комнат нужно для поселения 67 иногородних студентов?
→ Узнать ответ
Задание 2. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) масса активного вещества в таблетке
лекарства
Б) масса Земли
В) масса молекулы водорода
Г) масса взрослого слона
ЗНАЧЕНИЯ
1) 3,3464 10−27 кг
2) 5 т
3) 500 мг
4) 5,9726 124 кг
→ Узнать ответ
Задание 3. На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба.
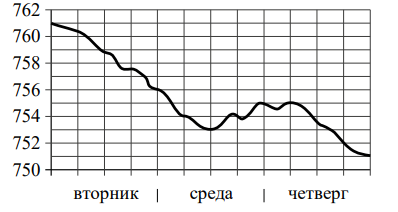
Определите по рисунку наибольшее значение атмосферного давления (в миллиметрах ртутного столба) в четверг.
→ Узнать ответ
Задание 4. Перевести температуру из шкалы Фаренгейта в шкалу Цельсия позволяет формула tc=5/9(tf-32) , где Ct — температура в градусах по шкале Цельсия, Ft — температура в градусах по шкале Фаренгейта. Скольким градусам по шкале Цельсия соответствует 356 градуса по шкале Фаренгейта?
→ Узнать ответ
Задание 5. В фирме такси в наличии 28 легковых автомобилей: 21 из них чёрного цвета с жёлтыми надписями на боках, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
→ Узнать ответ
Задание 6. В таблице 1 приведены минимальные баллы ЕГЭ по четырём предметам, необходимые для подачи документов на факультеты 1–6.
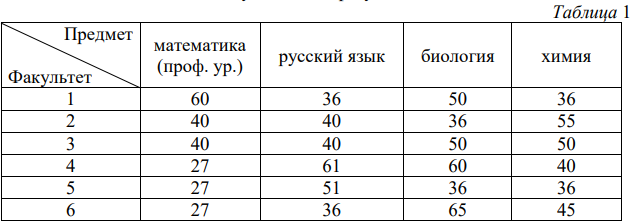
В таблице 2 приведены данные о баллах ЕГЭ по четырём предметам абитуриента В

Выберите факультеты, на которые может подавать документы абитуриент В. В ответе укажите номера всех выбранных факультетов без пробелов, запятых и других дополнительных символов.
→ Узнать ответ
Задание 7. Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1;1].
ГРАФИКИ
![Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1;1]. ГРАФИКИ](https://pndexam.ru/wp-content/uploads/2025/03/image-438.png)
ХАРАКТЕРИСТИКИ
1) Функция убывает на отрезке [−1;1].
2) Функция имеет точку минимума на отрезке [−1;1].
3) Функция имеет точку максимума на отрезке [−1;1].
4) Функция возрастает на отрезке [−1;1].
В таблице под каждой буквой укажите соответствующий номер.
→ Узнать ответ
Задание 8. В жилых домах, в которых больше 5 этажей, установлен лифт. Выберите утверждения, которые верны при приведённом условии.
1) Если в доме нет лифта, то в этом доме больше 6 этажей.
2) Если в доме лифта нет, то в этом доме меньше 6 этажей.
3) Если в доме больше 8 этажей, то в нём нет лифта.
4) Если в доме больше 7 этажей, то в нём есть лифт.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
→ Узнать ответ
Задание 9. План местности разбит на клетки. Каждая клетка обозначает квадрат 1м × 1м . Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
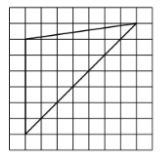
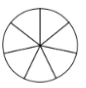
Задание 10. На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 18°?
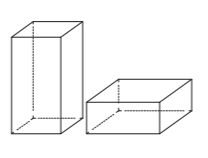
Задание 11. Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
Задание 12. В прямоугольнике одна из сторон равна 99, а диагональ равна 101. Найдите площадь этого прямоугольника.
Задание 13. Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 3 и 6, а второго — 4 и 9. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?