
Олимпиада «ВСОШ» ответы, вопросы по Информатике — Искусственный интеллект 7,8 класс, школьный этапа Всероссийской олимпиады г. Москвы от 24 октября 2025 года. Официальный вариант взятый с online.olimpiada
Школьный этап ВСОШ по Информатике для Москвы 24 октября 2025 г.
Вопросы и ответы 7-8 класс
Задания раздела: Искусственный интеллект
Задание 1. Пусть X — множество целых чисел, в котором nn элементов. Определим медиану mm множества X. Выпишем элементы множества X в порядке возрастания: a1<a2<…<an. При нечётном nn обозначим n=2k+1 и положим m=ak+1(т.,е. медиана — среднее из чисел в получившемся ряду). При чётном n обозначим n=2k и положим m=ak+ak+12 (т.,е. полагаем медиану — средним арифметическим двух средних чисел в получившемся ряду).
Пусть A и B — множества различных целых чисел, состоящие из нечётного числа элементов, причём A∩B=∅. Известно, что медиана множества A равна 10, а медиана множества B равна 100. Какое наибольшее значение может иметь медиана множества A∪B?
→ Раскрыть ответ
Задание 2. Три программы ИИ (искусственного интеллекта), отвечают на одни и те же 30 вопросов. Ансамбль из трёх программ выдаёт ответ на каждый вопрос «по правилу большинства»: если хотя бы две из трёх программ дали одинаковый ответ, выдаётся именнно этот ответ. В противном случае выдаётся ответ первой программы. Известно, что каждая из трёх программ ответила верно не менее чем на 2 вопроса. Какое наименьшее число правильных ответов гарантированно будет у ансамбля из трёх программ?
→ Раскрыть ответ
Задание 3. В порту расположено mm площадок, пронумерованных целыми числами 0,1,2,…,m−1. В порт прибудет контейнеровоз с сотней контейнеров, которые пронумерованы последовательными целыми числами. Автоматический кран разгружает контейнеровоз по следующему правилу: контейнер с номером N разгружается на площадку с таким номером kk, что N−k делится на m, напомним, что k принимает значения от 0 до m−1. При каком наибольшем значении m мы гарантированно можем утверждать, что на каждой площадке после разгрузки окажется не менее 99 контейнеров?
→ Раскрыть ответ
Задание 4. Вася настраивает проверку входящих писем по трём признакам A, B и C. Обозначим:
A — в письме есть слово БЕСПЛАТНО;
B — в письме есть три восклицательных знака подряд;
C — в письме есть ссылка (текстовый адрес, по которому открывается страница).
Письмо отправляется в папку НЕЖЕЛАТЕЛЬНАЯ ПОЧТА, если выполнены хотя бы два из трёх упомянутых выше признаков.
По набору писем известно, что признаки A и B выполнены одновременно для 80 писем, признаки A и C — для 50 писем, признаки B и C — для 60 писем. Все три признака A, B и C одновременно выполняются для 30 писем. Сколько писем отправится папку НЕЖЕЛАТЕЛЬНАЯ ПОЧТА?
→ Раскрыть ответ
Задание 5. Даны точки на клетчатой плоскости, разбитые на три класса:
класс 0: (2,−1), (1,1), (2,1), (1,−2), (2,0);
класс 1: (0,1), (−2,1), (−1,−2), (0,2);
класс 2: (−1,1), (0,−2), (−2,0).
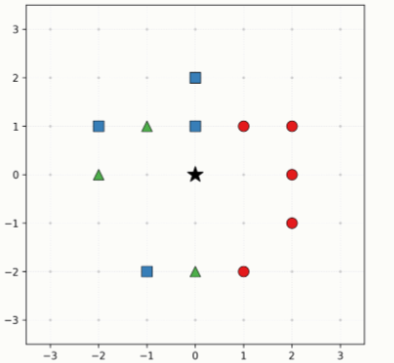
Рис. 1: Точки на плоскости
Новую точку (0,0), помеченную зведочкой, нужно отнести к одному из трех классов по правилу ближайшего центра, определим это правило далее.
Назовем центром класса точку, у которой первая координата равна среднему арифметическому всех первых координат точек класса, а вторая координата — среднему арифметическому всех вторых координат.
Ближайшим для точки считается класс, расстояние до центра которого наименьшее. В случае равенства нескольких расстояний ближайшим считается класс с меньшим номером.
Правило ближайшего центра требует относить точку к ближайшему для неё классу. Определите, какой класс получит точка, помеченная звёздочкой.
→ Раскрыть ответ
Задание 6. Линейный счётчик по модулю
| Имя входного файла: | стандартный ввод |
| Имя выходного файла: | стандартный вывод |
| Ограничение по времени: | 1 секунда |
| Ограничение по памяти: | 256 мегабайт |
В одной далёкой лаборатории учёные создали особого робота-предсказателя. Этот робот умеет строить магическую последовательность чисел. Его память устроена так: он всегда хранит два последних значения и по ним вычисляет следующее.
Работает он так:
F0=a,F1=b,Fn=(p⋅Fn−1+q⋅Fn−2)modm(n≥2)
Знак «modm» означает, что после вычисления берётся остаток от деления на число m.
Ваша задача — помочь роботу посчитать число Fn.
Формат входных данных
Ровно шесть строк:
1-я строка: целое n;
2-я строка: целое a;
3-я строка: целое b;
4-я строка: целое p;
5-я строка: целое q;
6-я строка: целое m.
Гарантируется, что
0≤n≤105, 1≤m≤109+7, 0≤a,b,p,q<m.
Формат выходных данных
Одно целое число — Fn.
→ Раскрыть ответ
Задание 7. Пожарная тревога
| Имя входного файла: | стандартный ввод |
| Имя выходного файла: | стандартный вывод |
| Ограничение по времени: | 1 секунда |
| Ограничение по памяти: | 256 мегабайт |
Представь, что у тебя есть карта города. На ней есть две пожарные станции: станция класса (0) с координатами (x0,y0) и станция класса (1) с координатами (x1,y1). Где-то в городе произошла авария, её место обозначено точкой (x,y).
Чтобы вызвать помощь, нужно понять, какая станция доберётся до аварии быстрее. Машины пожарных двигаются только вдоль улиц и проспектов, то есть сначала по горизонтали, потом по вертикали (или наоборот). Время проезда считается просто: складываем количество кварталов по горизонтали и по вертикали. Именно поэтому расстояние от точки ((u,v)) до точки (r,s) определяется так:
D((u,v),(r,s))=|u−r|+|v−s|
Нужно определить, какая станция по этому правилу ближе к месту аварии. Если обе станции окажутся на одинаковом расстоянии, помощь приедет со станции класса (0).
Формат входных данных
Шесть целых чисел, по одному в строке:
x, y, x0, y0, x1, y1
Гарантируется, что
|x|,|y|,|x0|,|y0|,|x1|,|y1|≤105.
Формат выходных данных
Выведите одно число: 0 или 1 — номер класса с меньшим расстоянием (при равенстве — 0).
→ Раскрыть ответ