
Официальный образец варианта заданий с ответами и решениями ВПР 2025 по Математике Базовый уровень 8 класс с официального ресурса ФИОКО (Федеральный институт оценки качества образования). Демоверсия предназначена для подготовки учащихся к всероссийской проверочной работе (ВПР), которая пройдет в период с 11 апреля по 16 мая 2025 года.
→ Типовые (тренировочные варианты) по Математике 10 класс
→ Образец проверочной работы по Математике 10 класс
→ Описание проверочной работы по Математике 10 класс
Онлайн вариант ВПР 2025 по Математике 10 класс
Назначение всероссийской проверочной работы
Всероссийские проверочные работы (ВПР) проводятся в целях осуществления мониторинга уровня и качества подготовки обучающихся в соответствии с требованиями федеральных государственных образовательных стандартов и федеральных основных общеобразовательных программ. Назначение ВПР по учебному предмету «Математика» – оценить качество общеобразовательной подготовки обучающихся 10 классов в соответствии с требованиями федерального государственного образовательного стандарта основного общего образования (ФГОС ООО) и федеральной образовательной программы основного общего образования (ФОП ООО).
Структура проверочной работы
Проверочная работа состоит из двух частей и включает в себя 17 заданий. В части 1 содержатся задания 1–12; в части 2 – задания 13–17. Во всех заданиях части 1 следует записать только ответ. Полное решение не является объектом проверки. В задании 15 следует построить график функции и ответить на вопрос задачи. В заданиях 13, 14, 16 и 17 объектом проверки является полное решение, то есть последовательность действий и рассуждений обучающегося.
Инструкция по выполнению работы
На выполнение заданий части 1 проверочной работы по математике отводится один урок (не более 45 минут). Часть 1 включает в себя 12 заданий. Ответы на задания запишите в поля ответов в тексте работы. В заданиях 4 и 6 нужно отметить точку на числовой прямой. Если Вы хотите изменить ответ, зачеркните его и запишите рядом новый. При выполнении работы не разрешается пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком. Записи в черновике проверяться и оцениваться не будут. Советуем выполнять задания в том порядке, в котором они даны. В целях экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения работы у Вас останется время, то Вы сможете вернуться к пропущенным заданиям.
Задания проверочной работы по Математике
Задание 1. В некотором городе 40 % населения интересуется футболом. Остальные горожане футболом не интересуются и футбольные матчи не смотрят. Среди тех, кто интересуется футболом, финальный матч чемпионата России смотрели 70 %. Сколько процентов горожан смотрели финальный матч?
Задание 2. Найдите значение выражения a^2/4√a^7*a^-4 при a = 81.
Задание 2. Найдите значение выражения a^-8/3 * a^5/a^2 при a=64
Задание 3. Вычислите: cos (-60)+sin^2 45
Задание 4. Найдите сумму бесконечно убывающей геометрической прогрессии 16, 8, 4, 2, 1, 1/2
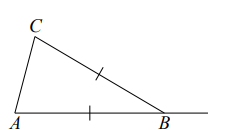
Задание 5. Известно, что в треугольнике ABC стороны AB и BC равны. Внешний угол при вершине B равен 138 . Найдите угол C. Ответ дайте в градусах.
Задание 6. Из коробки, в которой лежат 15 чёрных и 5 красных маркеров, достают один случайный маркер. Найдите вероятность того, что он окажется красным.
Задание 7. Каждый из 25 учащихся в классе посещает хотя бы один из двух кружков. Известно, что 10 человек занимаются в химическом кружке, а 18 в биологическом. Сколько учащихся посещают оба кружка?
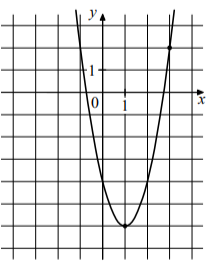
Задание 8. На рисунке изображён график функции f(x)=ax^2-4x+c.Найдите f(-3)
Задание 9. Симметричный игральный кубик бросили два раза. Известно, что при первом броске выпало больше очков, чем при втором. Какова вероятность того, что в сумме выпало семь очков?
Задание 10. Найдите tga, если sina=0.8 и π/2<a<π
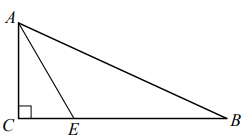
Задание 11. В прямоугольном треугольнике АВС с прямым углом С на стороне ВС отметили точку Е так, что ∠АЕВ=120 . Найдите АВ, если известно, что ВЕ=3, АС=√3.
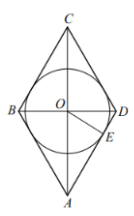
Задание 11. В ромбе ABCD диагонали пересекаются в точке О. Окружность радиусом 4 вписана в ромб и касается стороны AD в точке Е. Найдите площадь ромба, если известно, что DE = 2.
Задание 12. Дана четырёхугольная пирамида SABCD с вершиной S. Основание ABCD является прямоугольной трапецией с прямыми углами A и D. Отрезок SD перпендикулярен плоскости основания. Выберите из предложенного списка пары перпендикулярных прямых. 1) прямые SA и АВ 2) прямые SA и DB 3) прямые AB и SC 4) прямые SD и CB В ответе запишите номера выбранных пар прямых без пробелов, запятых и других дополнительных символов.
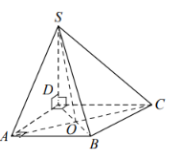
Задание 12. Дана четырёхугольная пирамида SABCD, в основании которой лежит квадрат ABCD. Диагонали квадрата пересекаются в точке O, и отрезок SO перпендикулярен плоскости основания. Точка М — середина стороны CD. Выберите из предложенного списка пары перпендикулярных прямых. 1) прямые SМ и АВ 2) прямые BS и DC 3) прямые SA и DB 4) прямые AB и SO 5) прямые AB и CB В ответе запишите номера выбранных пар прямых без пробелов, запятых и других дополнительных символов.
Инструкция по выполнению заданий части 2 проверочной работы
На выполнение заданий части 2 проверочной работы по математике отводится один урок (не более 45 минут). Часть 2 включает в себя 5 заданий. В заданиях 13, 14, 16, 17 запишите решение и ответ в указанном месте. В задании 15 постройте график функции и ответьте на поставленный вопрос. Если Вы хотите изменить ответ, зачеркните его и запишите рядом новый. При выполнении работы не разрешается пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком. Записи в черновике проверяться и оцениваться не будут. Советуем выполнять задания в том порядке, в котором они даны. В целях экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения работы у Вас останется время, то Вы сможете вернуться к пропущенным заданиям.
Задание 13. 1) Решите уравнение cos^2=cosx
2) Найдите корни этого уравнения, принадлежащие отрезку [12; 15].
Задание 14. Решите неравенство 3x^2-2x-1/5x+1 <= 0
Задание 15. Дана функция f(x)=||x|-3|+2
1) Постройте график функции y=f(x)
2) При каких значениях с уравнение f(x)=c имеет ровно три решения?
Задание 16. Дан прямоугольный параллелепипед abcda1b1c1d1 , в котором грань ABCD является квадратом. Известно, что AB = 8, АА1 =√105. Найдите косинус угла между прямыми А1D и AC.
Задание 16. Дана треугольная пирамида SABC с вершиной в точке S. Треугольник ABC равносторонний с центром точке O. Отрезок SO перпендикулярен плоскости основания. Известно, что AB = 6, а sa=4√3.Найдите расстояние от точки S до плоскости ABC
Задание 17. Баскетболист два раза бросает мяч в кольцо. При первом броске вероятность попадания равна 0,4. Если баскетболист промахнулся при первом броске, то при втором броске вероятность попадания не меняется, а если попал в кольцо, то при втором броске вероятность попадания равна 0,7. Какова вероятность того, что баскетболист попадёт мячом в кольцо ровно один раз?
Задание 17. В серии из 11 испытаний Бернулли вероятность успеха в каждом отдельном испытании равна 0,2. Во сколько раз вероятность события A «наступит ровно 4 успеха» меньше вероятности события B «наступит ровно 3 успеха»?