
Официальный образец варианта заданий с ответами и решениями ВПР 2025 по Математике Углубленный уровень 8 класс с официального ресурса ФИОКО (Федеральный институт оценки качества образования). Демоверсия предназначена для подготовки учащихся к всероссийской проверочной работе (ВПР), которая пройдет в период с 11 апреля по 16 мая 2025 года.
→ Типовые (тренировочные варианты) по Математике Углубленный уровень 8 класс
→ Образец проверочной работы по Математике Углубленный уровень 8 класс
→ Описание проверочной работы по Математике Углубленный уровень 8 класс
Онлайн вариант ВПР 2025 по Математике Углубленный уровень 8 класс
Назначение всероссийской проверочной работы
Всероссийские проверочные работы (ВПР) проводятся в целях осуществления мониторинга уровня и качества подготовки обучающихся в соответствии с требованиями федеральных государственных образовательных стандартов и федеральных основных общеобразовательных программ. Назначение ВПР по учебному предмету «Математика» – оценить качество общеобразовательной подготовки обучающихся 8 классов в соответствии с требованиями федерального государственного образовательного стандарта основного общего образования (ФГОС ООО) и федеральной образовательной программы основного общего образования (ФОП ООО).
Структура проверочной работы
Проверочная работа состоит из двух частей и включает в себя 16 заданий. Часть 1 состоит из заданий 1–10. В заданиях 1–3, 5–10 следует записать только ответ. Полное решение не является объектом проверки. В задании 4 требуется отметить точку на числовой прямой. Часть 2 состоит из заданий 11–16. В заданиях части 2 объектом проверки является полное решение, то есть последовательность действий и рассуждений обучающегося.
Инструкция по выполнению работы
На выполнение заданий части 1 проверочной работы по математике отводится один урок (не более 45 минут). Часть 1 включает в себя 10 заданий. Ответы на задания запишите в поля ответов в тексте работы. В задании 4 нужно отметить точку на числовой прямой. Если Вы хотите изменить ответ, зачеркните его и запишите рядом новый. При выполнении работы не разрешается пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком. Записи в черновике проверяться и оцениваться не будут. Советуем выполнять задания в том порядке, в котором они даны. В целях экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения работы у Вас останется время, то Вы сможете вернуться к пропущенным заданиям.
Задания проверочной работы по Математике Углубленный уровень
Задание 1. Найдите значение выражения √32*√6/√12
Задание 2. Решите уравнение x2-36=5x
Задание 3. Укажите номер утверждения, которое является истинным высказыванием.
1) Любой параллелограмм, в котором две стороны равны, является ромбом.
2) Любой четырёхугольник, в котором две диагонали равны и перпендикулярны, является
квадратом.
3) Любой параллелограмм, в котором диагонали равны, является прямоугольником.
4) В любой трапеции оба угла при меньшем основании тупые
Задание 4. На числовой прямой отмечены числа a и b . Отметьте на прямой какую-нибудь точку x так, чтобы при этом выполнялись три условия: x-a>0, x-b<0 и a^2x>0
Задание 5. В ромбе KLMN диагонали пересекаются в точке T. Из точки T опущен перпендикуляр TH на сторону KN. Найдите тупой угол ромба, если ∠LTH=153 . Ответ дайте в градусах.
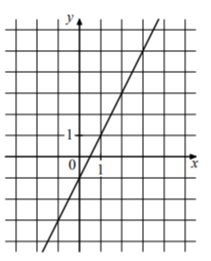
Задание 6. На рисунке изображён график линейной функции. Напишите формулу, которая задаёт эту линейную функцию.
Задание 7. Найдите значение выражения 2x/x-4 — 2x^2-32/x^2-8x+16 при x=3.96
Задание 8. При формировании продуктового заказа сборщик кладёт в пакет примерно 3 кг картофеля. Расположите следующие события в порядке возрастания их вероятностей.
A «Масса картофеля в пакете составляет от 2,9 до 3,2 кг».
B «Масса картофеля в пакете отклоняется от 3 кг не более чем на 100 г».
C «Масса картофеля в пакете отклоняется от 3 кг не более чем на 200 г».
D «Масса картофеля в пакете составляет от 2,5 до 3,5 кг».
Задание 9. В графе 14 рёбер. Каждая вершина графа имеет или степень 2, или степень 5. Причём вершин степени 2 столько же, сколько вершин степени 5. Сколько вершин в этом графе?
Задание 10. Число A является суммой квадратов трёх последовательных натуральных чисел. Найдите остаток от деления числа A на 3.
Инструкция по выполнению заданий части 2 проверочной работы
На выполнение заданий части 2 проверочной работы по математике отводится один урок (не более 45 минут). Часть 2 включает в себя 6 заданий. Во всех заданиях запишите решение и ответ в указанном месте. Если Вы хотите изменить ответ, зачеркните его и запишите рядом новый. При выполнении работы не разрешается пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком. Записи в черновике проверяться и оцениваться не будут. Советуем выполнять задания в том порядке, в котором они даны. В целях экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения работы у Вас останется время, то Вы сможете вернуться к пропущенным заданиям.
Задание 11. Решите неравенство 2x-3/5 — 4x-7/15 > 8x-7/3
Задание 12. Правильный игральный кубик бросают два раза. Найдите вероятность того, что сумма выпавших очков окажется не меньше 9.
Задание 13. Решите уравнение (X-3)^4-4(X-3)^2-5=0
Задание 14. Корнем квадратного уравнения 2x^2+3√2*x+c=0 является число √2-1. Найдите второй
корень данного уравнения.
Задание 14. Боковая сторона равнобедренного треугольника ABC равна 3, а основание AC равно 2. В этом треугольнике провели биссектрисы AL и CM . Найдите длину отрезка LM .
Задание 15. Расстояние между пунктами А и В по реке равно 11 км. Из пункта А в пункт В одновременно отправились плот и моторная лодка. Моторная лодка, прибыв в пункт В, тотчас повернула обратно. В двух километрах от пункта А лодка встретила плот. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.
Задание 16. Расстояние между пунктами А и В по реке равно 11 км. Из пункта А в пункт В одновременно отправились плот и моторная лодка. Моторная лодка, прибыв в пункт В, тотчас повернула обратно. В двух километрах от пункта А лодка встретила плот. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.
Задание 16. Боковые стороны AB и CD прямоугольной трапеции ABCD равны соответственно 40 и 41. Биссектриса угла ADC проходит через середину стороны AB . Найдите площадь трапеции.