
Олимпиада «Сириус» ответы, вопросы по Математике 9 класс, школьный этапа Всероссийской олимпиады 1 группа от 15 октября 2025 года. Официальный вариант с вопросами на логику, головоломки.
Школьный этап Сириус по Математике для 1-ой группы 15 октября 2025 г.
Вопросы и ответы 9 класс
Задание 1. Жора решал уравнение 19x=b, где неизвестная переменная x, а b некоторое число. Когда он увеличил коэффициент при x и число в правой части на 1, корень уравнения тоже увеличился на 1. На сколько увеличился бы корень уравнения, если бы Жора вместо этого увеличил коэффициент при x и число в правой части на 3?
→ Раскрыть ответ
Задание 1. Жора решал уравнение 11x = b, где неизвестная переменная 2, а b — некоторое число. Когда он увеличил коэффициент при х и число в правой части на 1, корень уравнения тоже увеличился на 1. На сколько увеличился бы корень уравнения, если бы Жора вместо этого увеличил коэффициент при 2 и число в правой части на 7?
→ Раскрыть ответ
Задание 1. Жора решал уравнение 13х = 6, где неизвестная переменная х, а в — некоторое число. Когда он увеличил коэффициент при х и число в правой части на 1, корень уравнения тоже увеличился на 1. На сколько увеличился бы корень уравнения, если бы Жора вместо этого увеличил коэффициент при х и число в правой части на 5?
→ Раскрыть ответ
Задание 2. Про натуральное число A известно, что оно делится на 50 и не делится на 75, а про натуральное число B известно, что оно делится на 60 и не делится на 90. Какие утверждения о числе C=A−B могут быть верны? Выберите все подходящие варианты:
C делится на 100
C не делится на 75
C не делится на 10
C делится на 6
C делится на 5
→ Раскрыть ответ
Задание 2. Про натуральное число А известно, что оно делится на 24 и не делится на 36, а про натуральное число В известно, что оно делится на 30 и не делится на 60. Какие утверждения о числе C = A — B могут быть верны? Выберите все подходящие варианты:
С делится на 6
C не делится на 12
С делится на 4
С не делится на 35
C не делится на 3
→ Раскрыть ответ
Задание 2. Про натуральное число А известно, что оно делится на 60 и не делится на 90, а про натуральное число В известно, что оно делится на 36 и не делится на 48. Какие утверждения о числе C = А — В могут быть верны? Выберите все подходящие варианты:
С делится на 18
С не делится на 4
С не делится на 9
С делится на 6
С не делится на 20
→ Раскрыть ответ
Задание 3. У Ивана есть большая корзина с 940 шариками одинакового размера. Как минимум один из шариков красный, остальные — зелёные. Иван вычислил, что вероятность того, что два случайно выбранных шарика окажутся красными, совпадает с вероятностью того, что они будут разного цвета. Сколько красных шариков в корзине?
→ Раскрыть ответ
Задание 3. У Ивана есть большая корзина с 970 шариками одинакового размера. Как минимум один из шариков красный, остальные зелёные. Иван вычислил, что вероятность того, что два случайно выбранных шарика окажутся красными, совпадает с вероятностью того, что они будут разного цвета. Сколько красных шариков в корзине?
→ Раскрыть ответ
Задание 3. У Ивана есть большая корзина с 880 шариками одинакового размера. Как минимум один из шариков красный, остальные зелёные. Иван вычислил, что вероятность того, что два случайно выбранных шарика окажутся красными, совпадает с вероятностью того, что они будут разного цвета. Сколько красных шариков в корзине?
→ Раскрыть ответ
Задание 4. Периметр трапеции ABCD (AD BC) равен 60, а расстояние между основаниями — 7 длина отрезка AB указана на рисунке.
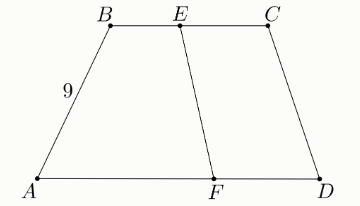
Периметры четырёхугольников ABEF и CDFE равны; площади этих четырёхугольников также равны.
Найдите длину отрезка CD.
Найдите площадь четырёхугольника ABCD.
→ Раскрыть ответ
Задание 4. Периметр трапеции ABCD (AD BC) равен 90, а расстояние между основаниями — 6 длина отрезка AB указана на рисунке.

Периметры четырёхугольников ABEF и CDFE равны; площади этих четырёхугольников также равны.
Найдите длину отрезка CD.
Найдите площадь четырёхугольника ABCD.
→ Раскрыть ответ
Задание 4. Периметр трапеции ABCD (AD BC) равен 80, а расстояние между основаниями — 4 длина отрезка AB указана на рисунке.

Периметры четырёхугольников ABEF и CDFE равны; площади этих четырёхугольников также равны.
Найдите длину отрезка CD.
Найдите площадь четырёхугольника ABCD.
→ Раскрыть ответ
Задание 5. Про действительные числа a, b и c известно, что 2⋅(2a√5+b√15+c√19)=a2+b2+c2+54.
Найдите значение выражения a2+b2+2c2.
→ Раскрыть ответ
Задание 6. Окружности Ω и ω пересекаются в точках A и B O центр окружности ω. Лучи CA и CB пересекают окружность Ω в точках D и E соответственно. Оказалось, что точка OК лежит на отрезке EC. На рисунке указаны значения углов ∠BCA и ∠BDA. Найдите градусную меру угла ∠EAB.
→ Раскрыть ответ
Задание 7. На большой клетчатой плоскости можно размещать прямоугольники размером 4×9 так, что каждый прямоугольник покрывает ровно 36 клеток. Прямоугольники можно размещать как горизонтально, так и вертикально, при этом они могут перекрываться
Найдите наибольшее целое число N, при котором невозможно покрыть ровно N клеток таким способом.
→ Раскрыть ответ
Задание 8. Исследователи опросили N человек, чтобы узнать, какие из трёх продуктов по уходу за кожей A , B , C они используют. Результаты опроса: 39 человек используют B; 59 человек НЕ пользуются A ; 24 человека НЕ пользуются C; 58 человек используют как минимум два из трёх видов A, B , C. Каждый человек мог выбрать любую комбинацию средств (в том числе не выбрать ни одно). Найдите минимально возможное значение N.
→ Раскрыть ответ